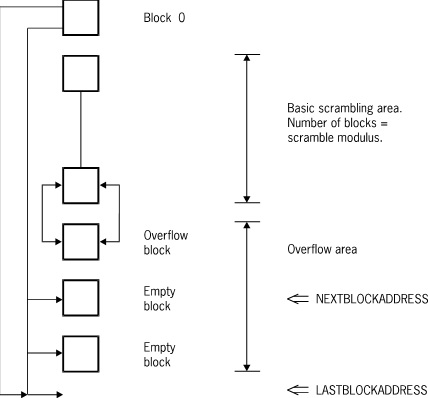
The following figure illustrates a random data set.
Random Data Set Description
Records in a random data set are not maintained in logical order, but they are allocated to particular blocks based on their key value.
Blocks 1 through m, where m is the modulus of the access, serve as the basic scrambling area. These blocks, along with block 0, are initialized when the data set is first established. When a record is created or retrieved, the key of the record key is folded and hashed. The result is a value between 1 and m that determines which of the basic blocks the record belongs to. In general, many key values can have the same hash value and belong to the same basic block.
Folding Algorithm for Random Data Sets
The folding algorithm for the random data set looks as follows:
B : = ((...(BOOLEAN(SK0[0])).[2: 48] EQV
BOOLEAN(SK0[1])).[2: 48] EQV
.
.
.
BOOLEAN(SK0[N]);
(NOTE: SK0 is the system key area.)
BLOCK ADDRESS IN THE BASIC AREA =
SEGSPERBLOCK*
INTEGER(REAL(((REAL(B).[47: 38] +
REAL(B).[9: 10]) MUX 4"26CE2036255B") MOD 1)*
MODULUS + .5)
(NOTE: The constant is related to the golden
ratio so that the value computer is insensitive
to the scramble modulus.)
FOLD : = -REAL(B.[47: 46] EQV B.[1: 2]);
(NOTE: FOLD.[47: 2] = 2)For more details of the folding algorithm, refer to The Art of Computer Programming, Sorting, and Searching, Volume 3, by Donald E. Knuth.
New records are inserted in the basic block so long as empty spaces are available in it. Within blocks, records are not maintained in order. If the basic block is full and an insertion is required, an overflow block is allocated and linked to the basic block. Additional overflow blocks are allocated as existing overflow blocks are filled. The result is a two-way circularly linked list of data blocks with the basic block at its head. Each basic block can potentially have its own chain of overflow blocks.
All basic blocks and overflow blocks are identical in format.
Data Block Format
The following figure illustrates the data block format of a random data set.
WORD
0 NEXTBLOCKLOC
1 PRIORBLOCKLOC
2 ---
.
. Fold words
.
---
---
.
.
.
. Records
.
.
.
---
NEXTBLOCKLOC Layout
The following figure illustrates the NEXTBLOCKLOC layout of a random data set.
Example 20. Random Data Set NEXTBLOCKLOC Layout
A A A A A A A * B B B B
A A A A A A A * B B B B
A A A A A A A * B B B B
A A A A A A A * B B B B
A 47: 28 BAF
Next block address.
* 19: 04 Unused
Zeros
B 15: 16 NUMBEREMPTY
The number of available record
slots in this block.PRIORBLOCKLOC Layout
The following figure illustrates the PRIORBLOCKLOC layout of a random data set.
Example 21. Random Data Set PRIORBLOCKLOC Layout
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A 47: 28 BAF
Prior block address
* 19: 20 Unused
ZerosFold Word Layout
The following figure illustrates the fold word layout of a random data set.
Example 22. Random Data Set Fold Word Layout
A B B B B B B B B B B B
A B B B B B B B B B B B
B B B B B B B B B B B B
B B B B B B B B B B B B
A 47: 02 RANDCONTF
0 = Corresponding data record is in the
process of being deleted.
1 = Impossible.
2 = Corresponding data record is in use.
3 = Corresponding data record is available.
B 45: 46 FOLD
The folded key.Words 0 and 1 are control words used to link blocks. To simplify finding available space, word 0 also contains a count of the available record locations in the block. The remainder of each block is divided in two parts: a table of fold words and the actual data records. The fold words are in one-to-one positional correspondence with the record areas in the block. Each fold word contains one field indicating whether the corresponding record is valid and another field containing the folded key value of the record. Available and in-use records are located by performing a mask search of the fold words.
When all the records in an overflow block are deleted, the overflow block is put in a ~one-way linked list of empty blocks, the head of which resides in block 0. (Refer to “Common Features” earlier in this appendix for additional information.)
Random Data Set Restrictions
The following restrictions apply to random data sets:
-
Bit vectors cannot be declared.
-
Variable-format records are not allowed.
-
Random data sets must not be embedded.
-
One Access must be declared for each random data set.
-
Duplicates are allowed, but DUPLICATES FIRST or DUPLICATES LAST cannot be specified.
The restrictions on the random data sets are for the following reasons:
-
Random data set efficiency depends upon avoiding overflow blocks so that the majority of records can be found with one physical access. This requires a fairly even distribution of keys in blocks and a block size and modulus adequate to accommodate the records with extra space for distributional variances. The hashing algorithm gives fairly good results for all modulus values. In a completely random distribution, the distribution of records in blocks is approximated by the Poisson distribution. If the blocking factor is B and the mean number of records for each block is M, then the probability of getting an overflow block is the probability of getting B+1 or more records when the mean is M. This probability can be determined for specific values of M and B from a set of cumulative Poisson tables.
-
Random data sets waste some space whether there are overflow blocks or not. Disk space is traded for retrieval speed.
-
Record creation, deletion, and modification are fast provided overflow blocks are avoided.
-
The FIND NEXT and FIND PRIOR operations on the data set read the file in physical order. The fold words indicate which records are valid so that invalid records can be bypassed quickly. The blocking factor of the file affects the efficiency of retrieval.
-
The FIND NEXT and FIND PRIOR operations using the Access work in similar fashion except that all overflow blocks for a basic block are examined before the next basic block is retrieved.
-
A FIND AT operation, initiated by the Access, uses the key to select the basic block and then examines the fold words to find candidates for selection. If a match on a fold word is found, then the actual record is examined. If it does not match, the search through the fold words continues. Test-specifying equality operations, such as the FIND AT K = 10 operation, are efficient as long as there are few overflow blocks. However, since records are not maintained in order, statements such as FIND AT K > 10 result in a scan of the entire file.