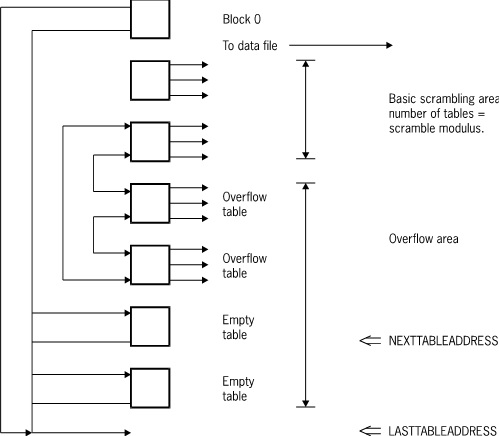
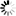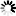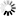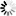The following figure illustrates index random sets and subsets.
Records in an index random set or subset are not maintained in key order, but they are allocated to particular tables based on their key value.
Tables 1 through m, where m is the modulus, serve as the basic scrambling area. These tables, along with block 0 (zero), are initialized when the set or subset is first established. When an entry is created or retrieved, its key value is folded and hashed. The result is a value between 1 and m that determines which of the basic tables the record belongs to. In general, many key values have the same hash value and belong to the same basic table.
Folding Algorithm for Index Random Sets and Subsets
The folding algorithm for index random sets and subsets looks as follows:
BOLD : = (...(BOOLEAN(SK0[0]).[2: 48] EQV
BOOLEAN(SK0[1])).[2: 48] EQV
.
.
.
BOOLEAN(SK0[N]);
(NOTE: SK0 is the system key area.)
FOLD : = ABS(REAL(BOLD.[47: 18]EQV BOLD).[31: 32]-1);
(NOTE: This is the folded key.)
BLOCK ADDRESS IN THE BASIC AREA =
SEGSPERBLOCK*
OLD MOD MODULUS) + 1);All basic tables and overflow tables are identical in format.
The hashing algorithm is sensitive to the value of MODULUS. For example, powers of 2 should be avoided.
Table Format
The following figure illustrates the table format for index random sets and subsets.
Example 34. Index Random Set and Subset Table Format
WORD
0 Table control word (TCW)
1 Table serial number (TSN)
2 NEXTBLOCKLOC
3 PRIORBLOCKLOC
4 Used for temporary storage not preserved.
5 ---
.
. Fold words for unused key entries.
.
---
---
.
. Fold words for in-use key entries in
. descending order on the fold part.
. (First is numbered one.)
.
---
---
.
. Fold words for unused key entries.
.
---
---
.
. In-use and unused key entries.
. One-to-one with fold words.
. Pointed to by pointer part of
fold words.
---Fold Word Layout
The following figure illustrates the fold word layout for index random sets and subsets.
Example 35. Index Random Set and Subset Fold Word Layout
A A A A B B B B B B B B
A A A A B B B B B B B B
A A A A B B B B B B B B
A A A A B B B B B B B B
A 47: 16 ENTRYLOCF
Pointer part containing offset to first
word of corresponding key entry.
B 31: 32 FOLDF
Fold part containing the folded key. NEXTBLOCKLOC Layout
The following figure illustrates the NEXTBLOCKLOC layout for index random sets and subsets.
Example 36. Index Random Set and Subset NEXTBLOCKLOC Layout
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A 47: 28 BAF
Next block address.
* 19: 20 Unused.
Zeros.PRIORBLOCKLOC Layout
The following figure illustrates the PRIORBLOCKLOC layout for index random sets and subsets.
Example 37. Index Random Set and Subset PRIORBLOCKLOC Layout
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A 47: 16 BAF
Prior block address.
* 19: 20 Unused.
Zeros.The first five words of each table are control words. The remainder of each table is divided in two parts: a table of fold words and the actual table entries.
One fold word exists in the table of fold words for each entry in the actual table (whether in use or not). Each fold word contains a fold part and a pointer part. The fold part contains the folded key value of the entry; the pointer part gives the offset to the first word of the actual table entry. Although the table entries themselves are not ordered, all in-use fold words are maintained in descending order on the fold part. This permits a binary search on the folded key values. When the desired folded key value is located in the fold table, the corresponding table entry can then be located using the pointer part of the fold word.
In-use fold words are always contiguous within the fold word table. Fold words float within the table under the control of the TCW located in word 0. Each TCW gives the location of the first in-use fold word and the number of valid fold words. (Refer to “Common Features” earlier in this appendix for TCW layout details.) The fine table bit in the TCW is not used for index random; it can contain any value.
When an entry is added to an index random set or subset, its basic table address is computed by folding and hashing the key. If there is room in the basic table, the table entry is inserted in the first available space, the fold word is inserted in the table of fold words by moving the entries ahead of it if necessary, and the TCW is updated.
| Note: | The fold words are conserved by the update. This preserves the one-to-one relationship between fold words and actual table entries. |
If there is no room, a table split is performed by allocating an overflow table, moving some of the entries from the old table to the new one, and linking the new table with the existing one. Additional overflow tables are allocated as existing tables are filled. The result is a two-way circularly linked list of tables with the basic table at its head. Each basic table can potentially have its own chain of overflow tables.
The number of entries moved from the old table to the new one depends solely upon the LOADFACTOR option. The LOADFACTOR option specifies the percentage of entries retained in the old table. For example, a LOADFACTOR value of 70 causes 70 percent of the entries to be retained in the old table and 30 percent of the entries to be moved to the new table. Note that the LOADFACTOR value is converted to entries, thus an individual entry is never split between tables.
The entries moved to the new table are always those with the highest fold values. As a result, fold words are maintained in sequence within each table, and tables are maintained in sequence within each chain. The next block link locates the table containing higher fold values; the prior block link locates the table containing lower fold values. The basic table always contains the lowest fold value.
If the database is audited, the TSN is used to coordinate the current state of the table with the audit trail. In unaudited databases, the TSN is present but not used.
When all of the entries in an overflow table are deleted, the table is put in a one-way linked list of empty blocks, the head of which resides in block 0. (Refer to “Common Features” earlier in this appendix for additional details.)
Index Random Set and Subset Restrictions
Index random sets and subsets cannot be embedded. This restriction exists for the following reasons:
-
Index random set and subset efficiency depends upon avoiding overflow tables so that the majority of records can be found with one physical access. This requires a fairly even distribution of keys in tables and TABLESIZE and MODULUS values adequate to accommodate the entries with extra space for distributional variances. The hashing algorithm gives poor results for even MODULUS values, therefore an odd value should be chosen. In a completely random distribution, the distribution of records in tables is approximated by the Poisson distribution. If the TABLESIZE value in entries is T and the mean number of entries for each table is M, then the probability of getting an overflow table is the probability of getting T+1 or more entries when the mean is M. This probability can be determined for specific values of M and T from a set of cumulative Poisson tables.
-
Index random sets and subsets waste some space if they are constructed to avoid overflow tables.
-
FIND NEXT and FIND PRIOR operations return the entries in the basic table in sequence by fold value and then return the entries in its overflow tables before retrieving the next basic table. Entries are not returned in order by key.
-
A FIND AT operation takes advantage of the two-part structure of the table. To find a particular entry, the appropriate basic table is first selected by folding and hashing the key of the entry. The resulting fold value is then compared to the table of fold words. Since fold values are in sequence within tables and overflow tables are maintained in sequence by fold value, the correct table can be selected by following the overflow chain. Then a binary search can be done on the fold words of that table. Only if a match occurs is a comparison against the actual key made. As with random data sets, only tests for equality, such as FIND AT K = 10, are efficient. Tests for inequality, such as FIND AT K > 10, result in a search of the entire index file.
-
When the distribution of keys is appropriate for an index random data set, a random data set could probably be used instead. The random data set would give faster access, but would waste more space on secondary storage. An index sequential data set, on the other hand, does provide an ordering and often provides random access performance comparable enough to an index random data set. The performance is comparable because the buffer management algorithm tends to keep coarse tables. Other advantages of index sequential data sets over index random data sets include efficient retrieval for inequality statements such as FIND AT K > 10 and the ability to use index sequential sets for embedded sets.