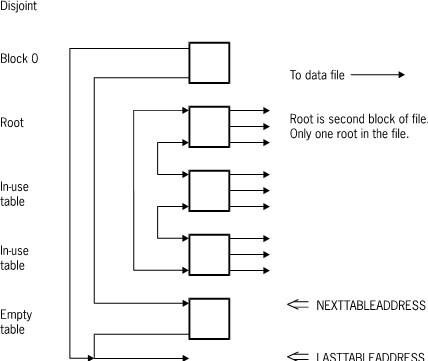
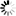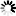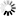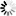The following figure illustrates ordered list sets and subsets.
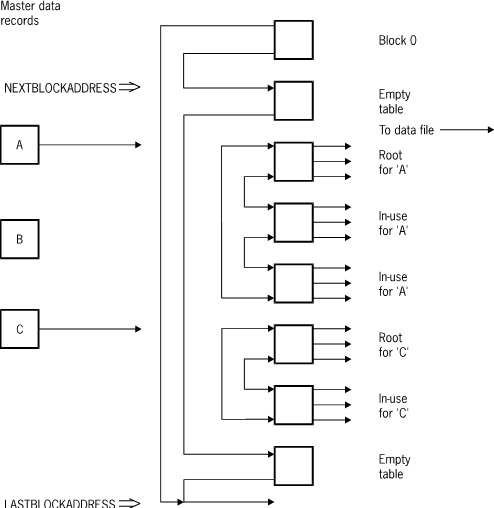
The following figure illustrates ordered list sets and subsets with embedded sets and subsets.
Ordered list sets and subsets are maintained in order by key. Entries reside in tables. One entry exists in the tables for each data set record contained in the set or subset.
Valid entries are always contiguous within tables. Within the range of valid entries, the entries are always in order by key. Thus the ordering allows a binary search to be used for insertion and retrieval when the proper table has been located. Entries are allowed to float within tables under the control of TCWs. Once the entries reach the beginning of the table, they are moved down to the end of the table. Each TCW gives the location of the first entry and the number of entries. Refer to “Common Features” earlier in this appendix for layout details. For ordered list sets and subsets, the fine table bit is meaningless and it can contain any value.
Tables are chained together to form a two-way circularly linked list. Within chains, tables are maintained in sequence. The next block link locates the table containing higher key values; the prior block link locates the table containing lower key values. For disjoint structures, there is one chain of tables. For embedded structures, there is one chain for each master, and each table contains entries belonging to only one master.
The root table always contains the lowest key value. For disjoint sets and subsets, the root table is always in block 2. For embedded sets and subsets, each root table is pointed to by its master.
Initially, there is one table containing only an Omega entry. The Omega entry is a system-created dummy key entry consisting of the highest key value (all ones).
Since entries are always maintained in sequence, a new entry must be placed in a particular position. To find that position, a FIND AT operation is implicitly performed. If there is room in the proper table, the entry is inserted there and the entries ahead of it are moved up. If there is no room, then a table split is performed by allocating a new table, moving some of the entries to the new table, and linking the new table in the chain.
Table splitting for ordered list sets and subsets is identical to table splitting for index sequential sets and subsets. Refer to “Index Sequential Sets and Subsets” earlier in this appendix for table splitting information.
Notice that tables are only split when they are full and a new entry must be inserted. In the embedded case, a split under one master does not cause a split under others.
Table Format
The following figure illustrates the table format for ordered list sets and subsets.
Example 40. Ordered List Set and Subset Table Format
WORD
0 Table control word (TCW)
1 Table serial number (TSN)
2 NEXTBLOCKLOC
3 PRIORBLOCKLOC
4 ---
.
. Unused key entries.
.
---
---
.
. In-use key entries
. in ascending collating sequence.
. (First entry is numbered one.)
.
---
---
.
. Unused key entries.
.
---NEXTBLOCKLOC Layout
The following figure illustrates the NEXTBLOCKLOC layout for ordered list sets and subsets.
Example 41. Ordered List Set and Subset NEXTBLOCKLOC Layout
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A 47: 28 BAF
Block address of next block.
* 19: 20 Unused.
Zeros.PRIORBLOCKLOC Layout
The following figure illustrates the PRIORBLOCKLOC layout for ordered list sets and subsets.
Example 42. Ordered List Set and Subset PRIORBLOCKLOC Layout
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A A A A A A A * * * * *
A 47: 28 BAF
Block address of prior block.
* 19: 20 Unused.
Zeros.If the database is audited, the TSN is used to coordinate the current state of the table with the audit trail. In unaudited data bases, the TSN is present but not used.
Empty blocks arise from deleting all entries in a table. These blocks are kept in a one‑way linked list whose head is in block 0.
Ordered List Set and Subset Restrictions
For the following reasons there are no restrictions on ordered list sets and subsets:
-
Efficient disk space utilization depends upon keeping tables reasonably full. When the set or subset is initially loaded in either ascending or descending sequence, tables are LOADFACTOR percent full. Random additions can cause the average table loading to change. Reorganization can be used to reorder and compact the ordered list sets and subsets.
-
Tables for embedded structures are not shared between masters. Since the minimum table size is one segment, at least one segment is allocated for each master with details.
-
FIND NEXT and FIND PRIOR operations access entries sequentially within each table, and then follow the link to the next table. Entries are returned in order by key.
-
A FIND AT operation uses a binary search within individual tables, but must go from table to table sequentially. This operation is, therefore, less efficient for ordered list sets and subsets than for index sequential or index random sets and subsets when more than two tables are in the chain.
-
Both disjoint and embedded ordered list sets and subsets provide efficient sequential retrieval. Ordered list sets and subsets should be used for random retrieval only when there are relatively few records for each master in the embedded case or relatively few records in the disjoint structure.